Cracking the Code of Calculus: Simplifying Differentiation and Integration

This mathematical discipline delves into the study of rates of change and accumulation, making it an indispensable tool in various fields, from physics and engineering to economics and biology. At the heart of calculus lie two fundamental concepts: differentiation and integration. Let's see how we can demystify these concepts, making them more approachable and comprehensible!

‍

Differentiation: Unraveling Rate of Change

Differentiation is the process of finding the rate at which a quantity changes concerning another related quantity. In simpler terms, it allows us to determine how a function changes as its input changes. Consider a car's speed as an example. If we have a function that describes the car's position concerning time, differentiating that function will yield the car's velocity at any given moment.

‍

The derivative, denoted by 'd/dx,' represents the rate of change or slope of a function at a specific point. If we have a function f(x), its derivative f'(x) signifies how the function's value changes concerning changes in x. The derivative can be thought of as the "instantaneous rate of change" of a function.

‍

To calculate derivatives, various rules and techniques are employed, including the power rule, product rule, quotient rule, and chain rule. These rules enable us to tackle functions of different complexities, enabling the analysis of their behavior with precision.

‍

Integration: Accumulating Insights

Integration, the counterpart of differentiation, involves finding the accumulation or total of a quantity over a given interval. Imagine calculating the total distance traveled by the car in the example above during a specific time interval. This process of finding the accumulation involves integration. 

‍

The integral symbol, ∫, represents the process of integration. If we have a function f(x), its integral ∫f(x) dx signifies the accumulation of the function concerning x. Essentially, integration helps us discover the "area under the curve" of a function.

‍

‍

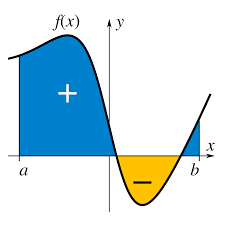
Integration techniques include the power rule for integration, integration by substitution, integration by parts, and partial fractions decomposition. By employing these techniques, we can handle various functions and scenarios where integration is required.

‍

Applications in Real Life

Calculus finds its applications in myriad real-life scenarios. In physics, calculus is indispensable for describing motion, modeling natural phenomena, and predicting behavior. Engineers use calculus to design structures, optimize systems, and analyze complex systems. Economists employ calculus to understand and model economic trends and behaviors.

‍

Medical researchers use calculus to model the spread of diseases and predict their progression. Even in day-to-day life, calculus plays a role; it helps us understand growth patterns, make informed decisions, and solve intricate problems.

‍

The Synergy of Differentiation and Integration

Differentiation and integration are closely intertwined. They are like two sides of the same coin, complementing each other to provide a comprehensive understanding of functions and their behavior. The Fundamental Theorem of Calculus establishes a profound relationship between these two concepts. It states that differentiation and integration are inverse operations. In other words, integration "undoes" differentiation and vice versa.

‍

‍

This synergy is the foundation of calculus and its applications. It empowers us to solve intricate problems, make predictions, and gain insights into the behavior of functions and systems.

‍

Mastering Calculus: A Step-by-Step Process

Mastering calculus involves building a solid foundation of these concepts and their applications. Start by understanding the basics of differentiation and integration, gradually working your way up to more complex functions and scenarios. Utilize resources such as textbooks, online tutorials, and practice problems to enhance your skills.

‍

Conceptual understanding is crucial in calculus. Focus on comprehending the principles behind differentiation and integration rather than rote memorization. Visual aids, graphs, and real-world examples can significantly aid your understanding.

‍

Conclusion

Calculus, often perceived as a complex and intimidating branch of mathematics, becomes more accessible when approached systematically. Differentiation and integration, the pillars of calculus, unlock a world of insights into the behavior of functions and their applications across various fields. By embracing these concepts and understanding their synergy, you embark on a journey of mathematical discovery that empowers you to solve problems, make predictions, and gain a deeper appreciation for the world around you.

‍

Want to discuss more about differentiation and integration with our state ranking tutors? Reach out to Concept at https://www.concepteducation.com.au/enquire or email us at admin@concepteducation.com.au - we're always happy to help!